Question

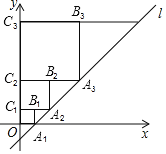
【题目】在平面直角坐标系中，直线l：y＝x﹣1与x轴交于点A，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnnCn+1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点B的坐标是_____，点Bn的坐标是_____．

Answer 1

【答案】(4，7) (2n﹣1，2n﹣1)

【解析】

根据一次函数图象上点的坐标特征找出A1、A2、A3、A4的坐标，结合图形即可得知点Bn是线段CnAn+1的中点，由此即可得出点Bn的坐标．

解：∵直线l：y＝x﹣1与x轴交于点A，

∴A1（1，0），

观察，发现：A1（1，0），A2（2，1），A3（4，3），A4（8，7），…，

∴An（2n﹣1，2n﹣1﹣1）（n为正整数）．

观察图形可知：B1（1，1），B2（2，3），B3（4，7），

点Bn是线段CnAn+1的中点，

∴点Bn的坐标是（2n﹣1，2n﹣1）．

故答案为：（4，7），（2n﹣1，2n﹣1）（n为正整数）．