题目内容
1.若实数m,m满足|m-2|+(n-2015)2=0,则m-1+n0=$\frac{3}{2}$.分析 根据非负数的和为零,可得每个非负数同时为零,根据负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1,可得答案.
解答 解:由m,m满足|m-2|+(n-2015)2=0,得
m-2=0,n-2015=0.
解得m=2,n=2015.
m-1+n0=$\frac{1}{2}$+1=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了非负数的性质,利用非负数的和为零得出每个非负数同时为零是解题关键,又利用了负整数指数幂、非零等零次幂.

练习册系列答案
相关题目
12.如果7x4-k=$\frac{1}{4}$y是二元一次方程,那么k的值是( )
| A. | 2 | B. | 3 | C. | 1 | D. | 0 |
10.下列图形中,是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 实数a和b在数轴上的对应点如图所示,化简:$\sqrt{{a}^{2}+4ab+4{b}^{2}}$+|a-b|.
实数a和b在数轴上的对应点如图所示,化简:$\sqrt{{a}^{2}+4ab+4{b}^{2}}$+|a-b|. 如图,AB∥CD,∠A=40°,∠1=70°,则∠C=30°.
如图,AB∥CD,∠A=40°,∠1=70°,则∠C=30°.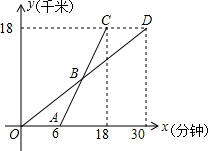 某校学生骑自行车从学校去某地植树,过了一段时间学校派后勤人员开车去送树苗和植树工具,学生、后勤人员离开学校的距离y(千米)与行驶时间x(分钟)的函数图象如图所示.
某校学生骑自行车从学校去某地植树,过了一段时间学校派后勤人员开车去送树苗和植树工具,学生、后勤人员离开学校的距离y(千米)与行驶时间x(分钟)的函数图象如图所示.