题目内容

【题目】如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．

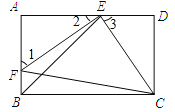
（1）求证：AE=DC；

（2）已知DC=，求BE的长．

【答案】（1）证明见试题解析；（2）2．

【解析】

试题（1）由矩形的性质及已知条件可得到△AEF≌△DCE，即可证明AE=DC；

（2）由（1）得到AE=DC，在Rt△ABE中由勾股定理可求得BE的长．

试题解析：（1）在矩形ABCD中，∠A=∠D=90°，∴∠1+∠2=90°，∵EF⊥EC，∴∠FEC=90°，∴∠2+∠3=90°，∴∠1=∠3，在△AEF和△DCE中，∵∠A=∠D，∠1=∠3，EF=EC，∴△AEF≌△DCE（AAS），∴AE=DC；

（2）由（1）得AE=DC，∴AE=DC=，在矩形ABCD中，AB=CD=，在R△ABE中，，即，∴BE=2．

练习册系列答案
相关题目

【题目】如图，在□ABCD中，AD是⊙O的弦，BC是⊙O的切线，切点为B．

（1）求证：；

（2）若AB＝5，AD＝8，求⊙O的半径．

【题目】如图1，矩形ABCD，AB=6cm，AD=8cm，点O从点B出发，以1cm/s的速度向点C运动，设O点运动时间为t（单位：s）（0<t<4），以点O为圆心，OB为半径作半圆⊙O交BC 于点M，过点A作⊙O的切线交BC于点N，切点为P.

（1）如图2，当点N与点C重合时，求t；

（2）如图3，连接AO，作OQAO交AN于点Q，连接QM，求证：QM是⊙O的切线；

（3）如图4，连接CP，在点O整个运动过程中，求CP的最小值.

【题目】如图，抛物线y＝ax2+bx+c（a≠0）与y轴交于点C，与x轴交于A，B两点，其中点B的坐标为B（4，0），抛物线的对称轴交x轴于点D，CE∥AB，并与抛物线的对称轴交于点E．现有下列结论：①a＞0；②b＞0；③4a+2b+c＜0；④AD+CE＝4．其中所有正确结论的序号是　_____________________ 　．

【题目】在Rt△ABC中，∠ACB＝90°，AC＝BC，CD为AB边上的中线．在Rt△AEF中，∠AEF＝90°，AE＝EF，AF＜AC．连接BF，M，N分别为线段AF，BF的中点，连接MN．

（1）如图1，点F在△ABC内，求证：CD＝MN；

（2）如图2，点F在△ABC外，依题意补全图2，连接CN，EN，判断CN与EN的数量关系与位置关系，并加以证明；

（3）将图1中的△AEF绕点A旋转，若AC＝a，AF＝b（b＜a），直接写出EN的最大值与最小值．

【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD的外角∠DAF的平分线．

（1）求证：AM是⊙O的切线；

（2）若∠D = 60°，AD = 2，射线CO与AM交于N点，请写出求ON长的思路．

【题目】如图，⊙O是△ABC的外接圆，AB经过点O，CD是弦，且CD⊥AB于点F，连接AD，过点B的直线与线段AD的延长线交于点E，且∠E=∠ACF．

（1）若CD=2， AF=3，求⊙O的周长；

（2）求证：直线BE是⊙O的切线．

【题目】（换元思想）阅读材料：

材料1 若一元二次方程的两根为、，则，.

材料2 已知实数、满足，，且，求的值.

解：由题知、是方程的两个不相等的实数根，根据材料1，得，.

∴.

根据上述材料解决下面的问题：

（1）一元二次方程的两根为，，则，___________；

（2）已知实数，满足，，且，求的值；

（3）已知实数，满足，，且，求的值.

【题目】如图，AB是⊙O的直径，且点C为⊙O上的一点，∠BAC=30°，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，且∠ECF=∠E．

（1）证明：CF是⊙O的切线；

（2）设⊙O的半径为1，且AC=CE，求MO的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网