Question

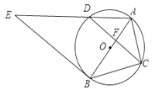
【题目】如图，⊙O是△ABC的外接圆，AB经过点O，CD是弦，且CD⊥AB于点F，连接AD，过点B的直线与线段AD的延长线交于点E，且∠E=∠ACF．

（1）若CD=2， AF=3，求⊙O的周长；

（2）求证：直线BE是⊙O的切线．

Answer 1

【答案】（1）8π；（2）证明见解析.

【解析】

（1）连接OC．设半径为r，在Rt△OFC中利用勾股定理即可解决问题．
（2）只要证明CD∥EB，即可得到∠AFD＝∠ABE＝90°，由此可以得出结论．

解：（1）连接OC．设半径为r，

∵OA⊥CD，

∴DF=FC=，

在RT△OFC中，∵∠OFC=90°，FC=，OF=r﹣3，OC=r，

∴r2=（r﹣3）2+（）2 ，

∴r=4，

∴⊙O的周长为8π．

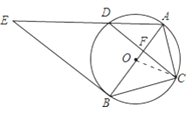
（2）证明：∵OA⊥CD，

∴DF=FC，AD=AC，∠AFD=90°

∴∠ADC=∠ACD，

∵∠E=∠ACD，

∴∠ADC=∠E，

∴CD∥EB，

∴∠AFD=∠ABE=90°，

∴BE是⊙O的切线．