题目内容
 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=3cm,BD=4cm
如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=3cm,BD=4cm(1)求该梯形的中位线的长;
(2)求该梯形的面积.
考点:梯形中位线定理,勾股定理
专题:
分析:(1)过点A作AE∥BD交CB的延长线于E,判断出四边形ADBE是平行四边形,根据平行四边形的对边相等可得BE=AD,AE=BD,再求出AC⊥AE,然后利用勾股定理列式求出CE,再根据梯形的中位线等于两底边和的一半列式计算即可得解;
(2)设点A到BC的距离为h,利用△ACE的面积列出方程求出h,再根据梯形的面积等于中位线乘高列式计算即可得解.
(2)设点A到BC的距离为h,利用△ACE的面积列出方程求出h,再根据梯形的面积等于中位线乘高列式计算即可得解.
解答: 解:(1)如图,过点A作AE∥BD交CB的延长线于E,
解:(1)如图,过点A作AE∥BD交CB的延长线于E,
∵AD∥BC,
∴四边形ADBE是平行四边形,
∴BE=AD,AE=BD=4cm,
∵AC⊥BD,BD∥AE,
∴AC⊥AE,
∴CE=
=
=5cm,
∴梯形的中位线=
(AD+BC)=
(BE+BC)=
CE=
cm,
即该梯形的中位线为
cm;
(2)设点A到BC的距离为h,
则S△ACE=
×5h=
×3×4,
解得h=
,
所以该梯形的面积=
×
=6.
 解:(1)如图,过点A作AE∥BD交CB的延长线于E,
解:(1)如图,过点A作AE∥BD交CB的延长线于E,∵AD∥BC,
∴四边形ADBE是平行四边形,
∴BE=AD,AE=BD=4cm,
∵AC⊥BD,BD∥AE,
∴AC⊥AE,
∴CE=
| AC2+AE2 |
| 32+42 |
∴梯形的中位线=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
即该梯形的中位线为
| 5 |
| 2 |
(2)设点A到BC的距离为h,
则S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| 12 |
| 5 |
所以该梯形的面积=
| 5 |
| 2 |
| 12 |
| 5 |
点评:本题考查了梯形的中位线等于两底边和的一半,勾股定理,三角形的面积,梯形的问题,作出合适的辅助线是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知|a|=3,|b|=
,且a<0<b,则a,b的值分别为( )
| 1 |
| 3 |
A、3,
| ||
B、-3,
| ||
C、-3,-
| ||
D、3,-
|
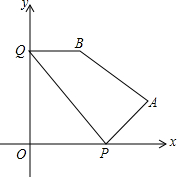 如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.
如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.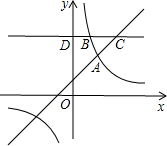 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y= 如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?
如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?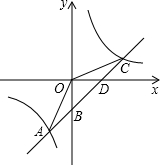 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=