题目内容
 如图,△ABC≌△EBD,点D在AB的延长线上,AC=BC,AO⊥AB于点O.已知AB=2,OC=3
如图,△ABC≌△EBD,点D在AB的延长线上,AC=BC,AO⊥AB于点O.已知AB=2,OC=3(1)求OD的长;
(2)分别求点E到AD、OC的距离.
考点:勾股定理,全等三角形的性质
专题:
分析:(1)根据等腰三角形三线合一的性质可得OA=OB,再利用勾股定理列式求出AC,然后根据全等三角形对应边相等可得BD=AC,最后根据OD=OB+BD代入数据计算即可得解;
(2)过点B作BM⊥AC于M,作EF⊥BD于F,作EG⊥OC于G,利用△ABC的面积列式求出BM,再根据全等三角形对应高相等可得EF=BM,再利用勾股定理列式求出BF,然后根据OF=OB+BF计算即可得解.
(2)过点B作BM⊥AC于M,作EF⊥BD于F,作EG⊥OC于G,利用△ABC的面积列式求出BM,再根据全等三角形对应高相等可得EF=BM,再利用勾股定理列式求出BF,然后根据OF=OB+BF计算即可得解.
解答: 解:(1)∵AC=BC,AO⊥AB,AB=2,
解:(1)∵AC=BC,AO⊥AB,AB=2,
∴OA=OB=
AB=
×2=1,
∵OC=3,△ABC≌△EBD,
∴BD=AC=
=
,
∴OD=OB+BD=1+
;
(2)如图,过点B作BM⊥AC于M,作EF⊥BD于F,作EG⊥OC于G,
则S△ABC=
AC•BM=
×2×3,
∴BM=
,
∴EF=BM=
,
即点E到AD的距离为
;
由勾股定理得,BF=
=
,
∴OF=OB+BF=1+
,
即点E到AC的距离为1+
.
 解:(1)∵AC=BC,AO⊥AB,AB=2,
解:(1)∵AC=BC,AO⊥AB,AB=2,∴OA=OB=
| 1 |
| 2 |
| 1 |
| 2 |
∵OC=3,△ABC≌△EBD,
∴BD=AC=
| 32+12 |
| 10 |
∴OD=OB+BD=1+
| 10 |
(2)如图,过点B作BM⊥AC于M,作EF⊥BD于F,作EG⊥OC于G,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=
3
| ||
| 5 |
∴EF=BM=
3
| ||
| 5 |
即点E到AD的距离为
3
| ||
| 5 |
由勾股定理得,BF=
22-(
|
| ||
| 5 |
∴OF=OB+BF=1+
| ||
| 5 |
即点E到AC的距离为1+
| ||
| 5 |
点评:本题考查了勾股定理,全等三角形对应边相等的性质,等腰三角形三线合一的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: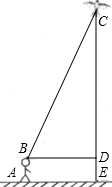 八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:
八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作: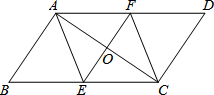 如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F.
如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.