题目内容
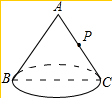
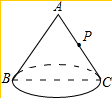如图所示，有一圆锥形粮堆，其正视图是边长为6m的正三角形ABC，粮堆母线AC的中点P处有一只老鼠正在偷吃粮食．此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是多少米？（结果不取近似值）分析：根据底面积圆的周长等于展开后扇形的弧长，得出圆心角进而得出B′P的长．
解答：
解：∵△ABC为正三角形，
∴BC=6，
∴l=2π×3=6π，
根据底面积圆的周长等于展开后扇形的弧长，得：
=6π，
故n=180°，则∠B′AC=90°，
∴B′P=
=3
（m），
答：小猫所经过的最短路程是3
米．
解：∵△ABC为正三角形，∴BC=6，
∴l=2π×3=6π，
根据底面积圆的周长等于展开后扇形的弧长，得：
| nπ×6 |
| 180 |
故n=180°，则∠B′AC=90°，
∴B′P=
| 36+9 |
| 5 |
答：小猫所经过的最短路程是3
| 5 |
点评：此题主要考查了圆锥的计算以及平面展开图最短路径问题，根据已知得出圆心角度数是解题关键．
练习册系列答案
相关题目
如图所示，有一圆锥形粮堆，其正视图是边长为6m的正三角形ABC，粮堆母线AC的中点P处有一只老鼠正在偷吃粮食．此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是多少米？（结果不取近似值）