Question

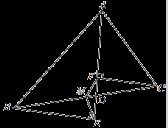
如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．

(1) 证明：∠BAC=∠DAC，∠AFD=∠CFE；

(2) 若AB∥CD，试证明四边形ABCD是菱形；

(3) 在(2)的条件下，试确定E点的位置，使∠EFD=∠BCD，并说明理由．

 

 

Answer 1

【解析】
(1) ∵AB=AD，CB=CD，AC=AC，

∴△ABC≌△ADC．

∴∠BAC =∠DAC．

∵ AB=AD，∠BAF =∠DAF，AF=AF．

∴△ABF≌△ADF．

∴∠AFB=∠AFD．

又∵∠CFE =∠AFB，

∴∠AFD=∠CFE．

∴∠BAC=∠DAC，∠AFD=∠CFE．

(2) ∵AB∥CD，

∴∠BAC=∠ACD．

又∵∠BAC=∠DAC，

∴∠BAC=∠ACD．

∴∠DAC=∠ACD．

∴AD=CD，

∵AB=AD ， CB=CD，

∴AB=CB=CD=AD．

∴四边形ABCD是菱形．

(3)当BE⊥CD时，∠EFD=∠BCD．理由：

∵四边形ABCD为菱形，

∴BC=CD，∠BCF=∠DCF．

又∵CF为公共边，

∴△BCF≌△DCF．

∴∠CBF=∠CDF，

∵BE⊥CD，

∴∠BEC =∠DEF=90°．

∴∠EFD =∠BCD．

 

【解析】

(1)利用已知条件和公共边，证得△ABC≌△ADC，即可证明∠BAC=∠DAC；再证明△ABF≌△ADF，得到∠AFB=∠AFD，再利用对顶角相等，易知结论；(2)有平行线的性质和(1)中结论，易知∠DAC=∠ACD，所以AD=CD，进而证得AB=CB=CD=AD，即可证明结论；(3)当BE⊥CD时，有(2)可知BC=CD ，∠BCF=∠DCF，利用△BCF≌△DCF证得∠CBF=∠CDF，再利用等角的余角相等即可证明结论∠EFD =∠BCD．