题目内容
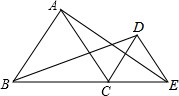 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,求BD与AE所成锐角的度数.
如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,求BD与AE所成锐角的度数.考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:由等边三角形的性质就可以得出△ACE≌△BCD,就可以得出∠CAE=∠CBD,∠CEA=∠CDB,由三角形外角与内角的关系就可以得出结论.
解答:解:∵△ABC与△CDE是等边三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=CE,
∴∠ACB+∠ACD=∠DCE+∠ACD,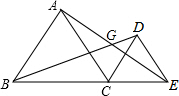
∴∠BCD=∠ACE.
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,∠CEA=∠CDB.
∵∠AGB=∠DBC+∠GEC,
∴∠AGB=∠CAE+∠GEC=∠ACB=60°.
答:BD与AE所成锐角的度数为60°.
∴∠ACB=∠DCE=60°,AC=BC,DC=CE,
∴∠ACB+∠ACD=∠DCE+∠ACD,

∴∠BCD=∠ACE.
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,∠CEA=∠CDB.
∵∠AGB=∠DBC+∠GEC,
∴∠AGB=∠CAE+∠GEC=∠ACB=60°.
答:BD与AE所成锐角的度数为60°.
点评:本题考查等边三角形性质的运用,三角形的外角与内角的关系的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
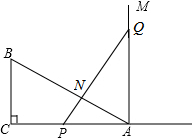 如图所示,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线上运动.问:
如图所示,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线上运动.问: