题目内容
2.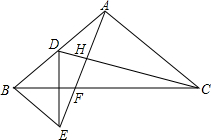 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,连接DE,探究BD与BE的数量关系并证明.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,连接DE,探究BD与BE的数量关系并证明.
分析 根据ASA证明△ABE≌△CAD,得到AD=BE,由点D是AB的中点,即可得到BD=BE.
解答 证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,
∴∠DAH=∠DCA,
∵∠BAC=90°,BE∥AC,
∴∠CAD=∠ABE=90°.
又∵AB=CA,
在△ABE与△CAD中,
$\left\{\begin{array}{l}{∠DAH=∠DCA}\\{∠CAD=∠ABE}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△CAD(ASA),
∴AD=BE,
又∵AD=BD,
∴BD=BE.
点评 本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
12.如果2(x+3)的值与3(1-x)的值互为相反数,那么x等于( )
| A. | 9 | B. | 2 | C. | 3 | D. | 4 |
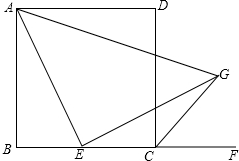 如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG.
如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG. 图中有三个正方形,请你指出图中所有的全等三角形.
图中有三个正方形,请你指出图中所有的全等三角形.