题目内容
18.方程组$\left\{\begin{array}{l}{3x+4y=2}\\{ax+\frac{b}{2}y=5}\end{array}\right.$与$\left\{\begin{array}{l}{\frac{a}{3}x-by=4}\\{2x-y=5}\end{array}\right.$有相同的解,求a、b的值.分析 因为两个方程组有相同的解,故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可.
解答 解:根据题意得;$\left\{\begin{array}{l}{3x+4y=2}\\{2x-y=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,
代入其他两个方程,
可得方程组$\left\{\begin{array}{l}{2a-\frac{b}{2}=5}\\{\frac{2a}{3}+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$.
点评 本题考查了学生对方程组有公共解定义的理解能力及应用能力,是一道好题,解决本题的关键是解二元一次方程组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.
如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.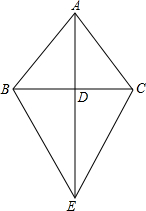 如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.
如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论. 如图,点E是平行四边形ABCD边BC上的一点,连接AC,DE,且AB=AE.
如图,点E是平行四边形ABCD边BC上的一点,连接AC,DE,且AB=AE.