��Ŀ����
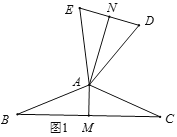
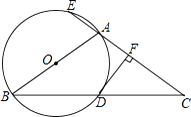
����:��ͼ1���ڡ�ABC�͡�ADE�У�AB=AC=AD=AE������BAC+��DAE=180��ʱ�����dzơ�ABC���DAE��Ϊ���������������Ρ�����ABC�ı�BC�ϵĸ���AM������ADE�ġ����ľࡱ����ADE�ı�DE�ϵĸ���AN������ABC�ġ����ľࡱ����A�������������ġ�.
������֪
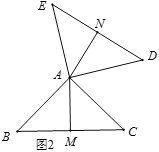
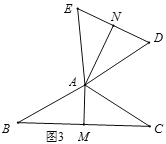
��1��ͼ2��ͼ3�У���ABC���DAE��Ϊ���������������Ρ���AM��AN�ǡ����ľࡱ,
����ͼ2������BAC=90��ʱ��AM��DE֮���������ϵΪAM=_________DE,
����ͼ3������BAC=120�㣬BC=6ʱ��AN�ij�Ϊ_________,
������֤
��2����ͼ1�У�����BACΪ�����ʱ������AM��DE֮���������ϵ��������֤��.
��չӦ��
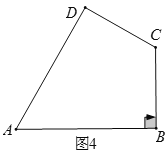
��3����ͼ4�����ı���ABCD�У�AD=AB��CD=BC����B=90�㣬��A=60�㣬CD=2�����ı���|ABCD���ڲ��Ƿ���ڵ�P��ʹ �á�PAD���PBC��Ϊ���������������Ρ�?�����ڣ������֤���������PBC�ġ����ľࡱ�ij����������ڣ� ��˵������.
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ


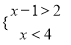 �Ľ⼯�ǣ�������
�Ľ⼯�ǣ�������
 =___________.
=___________.