题目内容
如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是_____.

【答案】
 .
.
【解析】
试题分析:根据正方形的性质以及勾股定理即可得出正方形对角线的长,进而得出线段O1O2中点G的运动路径的长.
试题解析:如图所示:

当P移动到C点以及D点时,得出G点移动路线是直线,
利用正方形的性质即线段O1O2中点G的运动路径的长就是O2O″的长,
∵线段AB=10,AC=BD=2,当P与C重合时,以AP、PB为边向上、向下作正方形APEF和PHKB,
∴AP=2,BP=8,
则O1P= ,O2P=4
,O2P=4 ,
,
∴O2P=O2B=4 ,
,
当P′与D重合,则P′B=2,则AP′=8,
∴O′P′=4 ,O″P′=
,O″P′= ,
,
∴H′O″=BO″= ,
,
∴O2O″=4 -
- =3
=3 .
.
故答案为:3 .
.
考点: 正方形的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


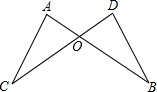 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.