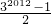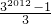题目内容
在求1+2+22+…+22010+22011的值时,可设S=1+2+22+…+22010+220①,则2S=2+22+23+…+22011+22012②,再由②-①得,S=22012-1.利用上述方法求1+3+32+…+32010+32011的值是( )
| A.32012-1 | B.32012-2 | C.
| D.
|
S=1+3+32+…+32010+32011①,
①×3得3S=3+32+…+32011+32012②,
②-①得2S=32012-1,
S=
.
故选C.
①×3得3S=3+32+…+32011+32012②,
②-①得2S=32012-1,
S=
| 32012-1 |
| 2 |
故选C.

练习册系列答案
相关题目