题目内容
求tan22.5°的值.
考点:解直角三角形
专题:
分析:构造图形如图,令AC=BC=1,∠ACB=90°,在Rt△ACB中求出∠D的正切值即可.
解答:解:构造图形:

如图,令AC=BC=1,∠ACB=90°,则AB=
,
延长CB至D,使得BD=AB,易得∠ADB=22.5°
∵在Rt△ACD中,AC=1,CD=1+
,
∴tan22.5°=
=
=
-1.

如图,令AC=BC=1,∠ACB=90°,则AB=
| 2 |
延长CB至D,使得BD=AB,易得∠ADB=22.5°
∵在Rt△ACD中,AC=1,CD=1+
| 2 |
∴tan22.5°=
| AC |
| CD |
| 1 | ||
1+
|
| 2 |
点评:本题考查学生对22.5°角是45°角的一半的认识程度,可考虑用万能公式,也可以从几何图形构造出22.5°的角进行求解.

练习册系列答案
相关题目
 如图,平行四边形ABCD的对角线交点O,直线l绕点O旋转与一组对边相交于点E,F.试说明:
如图,平行四边形ABCD的对角线交点O,直线l绕点O旋转与一组对边相交于点E,F.试说明: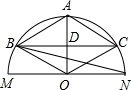 如图,MN为半圆O的直径,半径0A⊥MN,D为OA的中点,过点D作BC∥MN.求证:
如图,MN为半圆O的直径,半径0A⊥MN,D为OA的中点,过点D作BC∥MN.求证: 如图,把图中的四边形ABCD以点O为位似中心,沿AO方向放大到原来的2倍(即位似比为2).
如图,把图中的四边形ABCD以点O为位似中心,沿AO方向放大到原来的2倍(即位似比为2).