题目内容
【题目】下列每个图形都是由一些黑点和一些白点按一定的规律组成的．
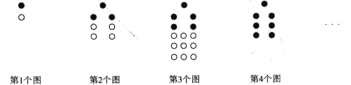
(1)根据规律，第4个图中有 个白点；第
个图形中，白点和黑点总数的和为 (用表示，为正整数)；
(2)有没有可能黑点比白点少2020个，如果有，求出此时的值；如果没有，请说明理由．
【答案】(1) 16；
； (2) 没有，理由见解析
【解析】
（1）由前3个图形中白点、黑点的个数得到规律，即可得到答案；
（2）根据（1）的结果列方程
求解解答即可.
解：(1)第1个图中白点1个，黑点1个，
第2个图中白点4=
个，黑点3=
个，
第3个图中白点9=
个，黑点5=1+个，
∴第4个图中白点
，黑点1+
=7个，
第n个图中白点
个，黑点
=2n-1个，
∴第
个图形中，白点和黑点总数的和为，
故答案为：16，；
(2)由图可知，第个图形的黑点个数为
，白点个数为.
若，即
，此时为无理数，故不存在这样的值使得黑点比白点少2020个.
练习册系列答案
相关题目
