题目内容
17．
如图，△ABC中，D，E分别上边AB，AC的中点，若DE=3，则BC=（ ）| A． | $\frac{3}{2}$ | B． | 9 | C． | 6 | D． | 5 |
分析 由已知条件得出DE是△ABC的中位线，根据三角形中位线定理即可得出BC=2DE．
解答 解：∵D，E分别上边AB，AC的中点，
∴DE是△ABC的中位线，
∴BC=2DE=6；
故选：C．
点评 本题考查了三角形中位线的定义和性质定理；熟练掌握三角形中位线定理，证明三角形中位线是解决问题的关键．
练习册系列答案
相关题目
如图，正比例函数y=2x与一次函数y=kx+4的图象交于点A（m，2），则不等式2x＜kx+4的解集为x＜1．
小军利用一张圆心角为90°，半径为20cm的扇形皮纸制作了一顶圆锥形纸帽（如下面的示意图），按照1：5的比例尺画出纸帽的三视图并标注数据．
2．某县10名学生参加汉字听写大赛，他们得分情况如下表：
那么这10名学生所得分数的中位数和众数分别是（ ）
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A． | 85和82.5 | B． | 85.5和85 | C． | 85和85 | D． | 85.5和80 |
9．
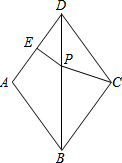如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（ ）
如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（ ）| A． | 108° | B． | 72° | C． | 90° | D． | 100° |
6．下列各项结论中错误的是（ ）
| A． | 二元一次方程x+2y=2的解可以表示为$\left\{\begin{array}{l}{x=m}\\{y=1-\frac{m}{2}}\end{array}\right.$ （m是实数） | |
| B． | 若$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{3x+2y=m}\\{nx-y=1}\end{array}\right.$的解，则m+n的值为0 | |
| C． | 设一元二次方程x2+3x-4=0的两根分别为m、n，则m+n的值为-3 | |
| D． | 若-5x2ym与xny是同类项，则m+n的值为3 |
如图，已知，如图∠1=∠2=40°，∠3=80°，则∠BAC=60°．