题目内容
19.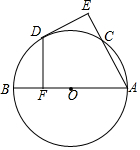 如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F.
如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F.(1)求证:DE是⊙O的切线;
(2)若OF=2,求AC的长度.
分析 (1)连接OD、AD.只要证明OD∥AE,由DE⊥AC,推出DE⊥OD即可解决问题;
(2)连接BC.只要证明△DFO∽△BCA,推出$\frac{OF}{AC}$=$\frac{OD}{AB}$=$\frac{1}{2}$即可解决问题;
解答 (1)证明:连接OD、AD.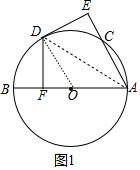
∵点D是$\widehat{BC}$的中点,
∴$\widehat{BD}$=$\widehat{AD}$,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AE,
∴∠AED=90°,
∴∠AED=∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)解:连接BC.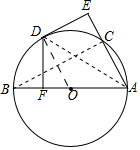
∵AB是⊙O直径,
∴∠ACB=90°,
∵OD∥AE,
∴∠DOB=∠EAB,
∵∠DFO=∠ACB=90°,
∴△DFO∽△BCA,
∴$\frac{OF}{AC}$=$\frac{OD}{AB}$=$\frac{1}{2}$,
即$\frac{2}{AC}$=$\frac{1}{2}$,
∴AC=4.
点评 本题考查切线的判定和性质、垂径定理、勾股定理、相似三角形的性质等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考常考题型.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
4.一个人从A地出发向北偏东80°方向到达B地,再从B地向北偏西25°方向到达C地,如果∠ACB=55°,则∠CAB的度数是( )
| A. | 25° | B. | 50° | C. | 70° | D. | 75° |
9.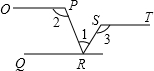 如图,已知OP∥QR∥ST,则下列等式中正确的是( )
如图,已知OP∥QR∥ST,则下列等式中正确的是( )
 如图,已知OP∥QR∥ST,则下列等式中正确的是( )
如图,已知OP∥QR∥ST,则下列等式中正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=180° | C. | ∠2+∠3-∠1=180° | D. | ∠1+∠2+∠3=180° |

 如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,且CD=BD.
如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,且CD=BD.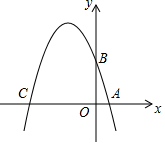 如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.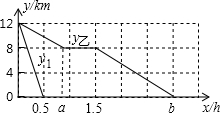 某景区内从甲地到乙地的路程是12km,小华步行从甲地到乙地游玩,速度为5km/h,走了4km后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是24km/h,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为y乙(km),第n趟电瓶车距乙地的路程为yn(km),n为正整数,行进时间为x(h).如图画出了y乙,y1与x的函数图象.
某景区内从甲地到乙地的路程是12km,小华步行从甲地到乙地游玩,速度为5km/h,走了4km后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是24km/h,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为y乙(km),第n趟电瓶车距乙地的路程为yn(km),n为正整数,行进时间为x(h).如图画出了y乙,y1与x的函数图象.