题目内容
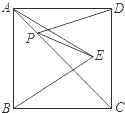
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. 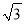 B. 2
B. 2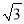 C. 2
C. 2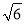 D.
D. 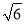
练习册系列答案
相关题目
某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
(1)21种.(2)y=-0.2x+280.x=40时成本总额最低. 【解析】 试题分析:(1)设生产A种饮料x瓶解出不等式方程组即可. (2)如图可得x与y的关系式,可知道x与y的关系. 试题解析:(1)根据题意得: , 解这个不等式组,得20≤x≤40. 因为其中正整数解共有21个, 所以符合题意的生产方案有21种. (2)根据题意,得y=...

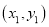 、
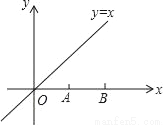
、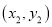 在直线
在直线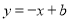 上,若
上,若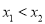 ,则
,则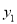 与
与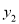 大小关系是( )
大小关系是( )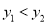 B.
B. 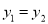 C.
C. 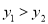 D. 无法确定
D. 无法确定
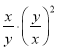 =________.
=________.