题目内容
 已知线段DE分别交△ABC的边AB、AC于D、E,且
已知线段DE分别交△ABC的边AB、AC于D、E,且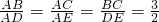 ,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.
,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.
解:∵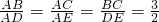 ,
,
∴ =
= ,△ADE∽△ABC
,△ADE∽△ABC
∵△ABC的周长是6cm,
∴ =
=
∴△ADE的周长:AD+AE+DE=4cm.
令△ADE的面积为S,则 =
=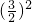 ,
,
∴S= cm2.
cm2.
分析:由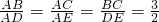 ,可知DE∥BC,△ADE∽△ABC;利用相似三角形的高的比、周长比等于相似比,面积比等于相似比的平方,此题可求.
,可知DE∥BC,△ADE∽△ABC;利用相似三角形的高的比、周长比等于相似比,面积比等于相似比的平方,此题可求.
点评:主要考查平行线分线段成比例定理和相似三角形的判定和性质,利用面积比等于相似比的平方.
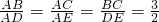 ,
,∴
 =
= ,△ADE∽△ABC
,△ADE∽△ABC∵△ABC的周长是6cm,
∴
 =
=
∴△ADE的周长:AD+AE+DE=4cm.
令△ADE的面积为S,则
 =
=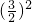 ,
,∴S=
 cm2.
cm2.分析:由
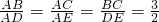 ,可知DE∥BC,△ADE∽△ABC;利用相似三角形的高的比、周长比等于相似比,面积比等于相似比的平方,此题可求.
,可知DE∥BC,△ADE∽△ABC;利用相似三角形的高的比、周长比等于相似比,面积比等于相似比的平方,此题可求.点评:主要考查平行线分线段成比例定理和相似三角形的判定和性质,利用面积比等于相似比的平方.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 已知线段DE分别交△ABC的边AB、AC于D、E,且
已知线段DE分别交△ABC的边AB、AC于D、E,且
 ,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.
,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.
 ,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.
,△ABC的周长是6cm,面积是2cm2,求△ADE的周长和面积.