题目内容
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.

证明:如图,∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,AC=BD,OD= BD,OC=
BD,OC= AC,
AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC﹣∠ODC=∠BCD﹣∠OCD,即∠EDO=∠FCO,
∴在△ODE与△OCF中, ,
,
∴△ODE≌△OCF(SAS),
∴OE=OF.

练习册系列答案
相关题目
正方形是轴对称图形,它的对称轴有( )
|
| A. | 2条 | B. | 4条 | C. | 6条 | D. | 8条 |
某篮球队12名队员的年龄如表:
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和平均数分别是( )
|
| A. | 18,19 | B. | 19,19 | C. | 18,19.5 | D. | 19,19.5 |
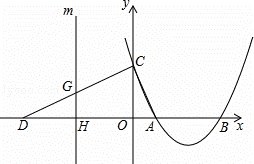
 的图象相交,其中有一个交点的横坐标是2,则k的值为
的图象相交,其中有一个交点的横坐标是2,则k的值为  ),AB=4
),AB=4 ,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.
,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.