题目内容
如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2 ),AB=4
),AB=4 ,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.
,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.
(1)求证:△AOD是等边三角形;
(2)求点B的坐标;
(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.
①当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围)
②若m=2,请直接写出此时直线l与x轴的交点坐标.

解:(1)如图2,证明:过点A作AM⊥x轴于点M,
∵点A的坐标为(2,2 ),
),
∴OM=2,AM=2
∴在Rt△AOM中,tan∠AOM= =
= =
=
∴∠AOM=60°
由勾股定理得,OA= =
= =4
=4
∵OD=4,
∴OA=OD,
∴△AOD是等边三角形.

(2)如图2,解:过点A作AN⊥BC于点N,
∵BC⊥OC,AM⊥x轴,
∴∠BCM=∠CMA=∠ANC=90°
∴四边形ANCM为矩形,
∴AN=MC,AM=NC,
∵∠B=60°,AB=4 ,
,
∴在Rt△ABN中,AN=AB•SinB=4 ×
× =6,BN=AB•CosB=4
=6,BN=AB•CosB=4 ×
× =2
=2
∴AN=MC=6,CN=AM=2 ,
,
∴OC=OM+MC=2+6=8,
BC=BN+CN=2 +2
+2 =4
=4 ,
,
∴点B的坐标为(8,4 ).
).


(3)①如图3,m=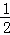 t+2;
t+2;
②如图4,(2,0),( ,0).
,0).

练习册系列答案
相关题目
如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )

|
| A. |
| B. |
| C. |
| D. |
|
下列运算正确的是( )
|
| A. | a3+a3=a6 | B. | a6÷a2=a4 | C. | a3•a5=a15 | D. | (a3)4=a7 |
 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ) 第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简,S1+S2+S3+…+S2014=
第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简,S1+S2+S3+…+S2014=






 .
.