题目内容
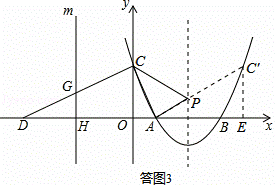
如图,抛物线y=ax2﹣8ax+12a(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(1)请直接写出A、B两点的坐标;
(2)求抛物线的解析式;
(3)抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标及周长的最小值;若不存在,说明理由;
(4)平行于y轴的直线m从点D出发沿x轴向右平行移动,到点A停止.设直线m与折线DCA的交点为G,与x轴的交点为H(t,0).记△ACD在直线m左侧部分的面积为s,求s关于t的函数关系式及自变量t的取值范围.
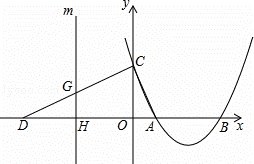
解:(1)抛物线的解析式为:y=ax2﹣8ax+12a(a>0),
令y=0,即ax2﹣8ax+12a=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)抛物线的解析式为:y=ax2﹣8ax+12a(a>0),
令x=0,得y=12a,∴C(0,12a),OC=12a.
在Rt△COD中,由勾股定理得:CD2=OC2+OD2=(12a)2+62=144a2+36;
在Rt△COD中,由勾股定理得:AC2=OC2+OA2=(12a)2+22=144a2+4;
在Rt△COD中,由勾股定理得:DC2+AC2=AD2;
即:(144a2+36)+(144a2+4)=82,
解得:a=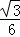 或a=﹣
或a=﹣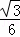 (舍去),
(舍去),
∴抛物线的解析式为:y=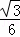 x2﹣
x2﹣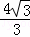 x+
x+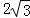 .
.
(3)存在.
对称轴为直线:x=﹣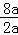 =4.
=4.
由(2)知C(0,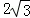 ),则点C关于对称轴x=4的对称点为C′(8,
),则点C关于对称轴x=4的对称点为C′(8,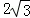 ),
),
连接AC′,与对称轴交于点P,则点P为所求.此时△PAC周长最小,最小值为AC+AC′.
设直线AC′的解析式为y=kx+b,则有:
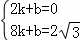 ,解得
,解得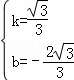 ,
,
∴y=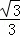 x﹣
x﹣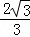 .
.
当x=4时,y=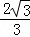 ,∴P(4,
,∴P(4,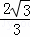 ).
).
过点C′作C′E⊥x轴于点E,则C′E=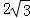 ,AE=6,
,AE=6,
在Rt△AC′E中,由勾股定理得:AC′=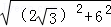 =4
=4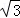 ;
;
在Rt△AOC中,由勾股定理得:AC=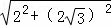 =4.
=4.
∴AC+AC′=4+4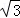 .
.
∴存在满足条件的点P,点P坐标为(4,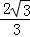 ),△PAC周长的最小值为4+4
),△PAC周长的最小值为4+4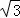 .
.
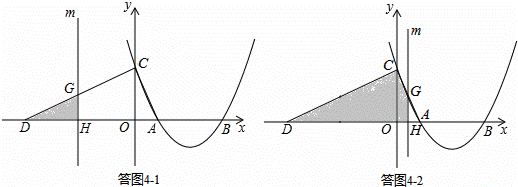
(4)①当﹣6≤t≤0时,如答图4﹣1所示.
∵直线m平行于y轴,
∴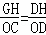 ,即
,即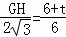 ,解得:GH=
,解得:GH=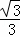 (6+t)
(6+t)
∴S=S△DGH=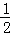 DH•GH=
DH•GH=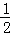 (6+t)•
(6+t)•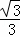 (6+t)=
(6+t)=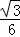 t2+2
t2+2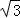 t+6
t+6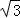 ;
;
②当0<t≤2时,如答图4﹣2所示.
∵直线m平行于y轴,
∴ ,即
,即 ,解得:GH=﹣
,解得:GH=﹣ t+2
t+2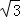 .
.
∴S=S△COD+S梯形OCGH=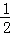 OD•OC+
OD•OC+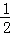 (GH+OC)•OH
(GH+OC)•OH
=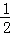 ×6×2
×6×2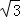 +
+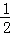 (﹣
(﹣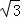 t+2
t+2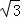 +2
+2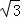 )•t
)•t
=﹣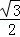 t2+2
t2+2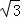 t+6
t+6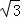 .
.
∴S=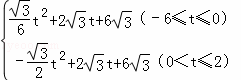 .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案在﹣2,0,3, 这四个数中,最大的数是( )
这四个数中,最大的数是( )
|
| A. | ﹣2 | B. | 0 | C. | 3 | D. |
|

 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ) 中,自变量x的取值范围是 .
中,自变量x的取值范围是 . C.
C.  D. 2
D. 2