题目内容
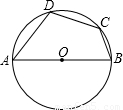
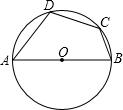已知：以AB为直径的半圆上有C、D两点，∠DCB=120°，∠ADC=105°，CD=1（如图），求四边形ABCD的面积．
解：如图，连接OD，OC．作CE⊥AB．
∵∠DCB=120°，
∴∠DAB=60°，
∴△OAD为等边三角形，
∴∠ODC=105°-60°=45°，
∴△OCD为等腰直角三角形，∠OCB=OBC=75°．
∵CD=1．
∴OD=
．CE=
=
∴△AOD面积=
（）2=
．
△ODC面积=
．
△OCB=
OB×CE=
．
∴四边形ABCD的面积=++=
．
分析：连接OD，OC．作CE⊥AB．从而得到△OAD为等边三角形，△OCD为等腰直角三角形，从而将四边形转化为特殊的三角形来求面积．
点评：本题考查了圆周角定理，利用圆周角定理得到特殊的角是解决本题的关键．
∵∠DCB=120°，
∴∠DAB=60°，
∴△OAD为等边三角形，
∴∠ODC=105°-60°=45°，
∴△OCD为等腰直角三角形，∠OCB=OBC=75°．
∵CD=1．
∴OD=
．CE==∴△AOD面积=
（）2=．△ODC面积=
．△OCB=
OB×CE=．∴四边形ABCD的面积=
++=．分析：连接OD，OC．作CE⊥AB．从而得到△OAD为等边三角形，△OCD为等腰直角三角形，从而将四边形转化为特殊的三角形来求面积．
点评：本题考查了圆周角定理，利用圆周角定理得到特殊的角是解决本题的关键．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知：以AB为直径的半圆上有C、D两点，∠DCB=120°，∠ADC=105°，CD=1（如图），求四边形ABCD的面积．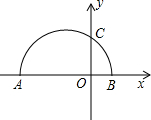
如图，已知A（-8，0），B（2，0），以AB为直径的半圆与y轴正半轴交于点C，则经过A、B、C三点的抛物线的解析式为
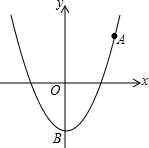如图，已知抛物线y=ax2+b经过点A（4，4）和点B（0，-4）．C是x轴上的一个动点．