题目内容
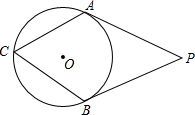如图，PA，PB，分别切⊙O于点A，B，∠P=70°，∠C等于________．
55°
分析：连接OA、OB，由切线的性质和圆周角定理即可求出∠C的度数．
解答：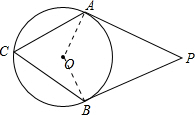
解：连接OA、OB，
∵PA、PB分别切⊙O于点A、B，
∴OA⊥PA、OB⊥PB，
∵∠P=70°，
∴∠AOB=110°，
∴∠C=55°，
故答案为：55°．
点评：本题主要考查了切线的性质、四边形的内角和、圆周角的有关定理，解题的关键在于作辅助线构建四边形，求出与∠C同弧的圆心角的度数．
分析：连接OA、OB，由切线的性质和圆周角定理即可求出∠C的度数．
解答：
解：连接OA、OB，∵PA、PB分别切⊙O于点A、B，
∴OA⊥PA、OB⊥PB，
∵∠P=70°，
∴∠AOB=110°，
∴∠C=55°，
故答案为：55°．
点评：本题主要考查了切线的性质、四边形的内角和、圆周角的有关定理，解题的关键在于作辅助线构建四边形，求出与∠C同弧的圆心角的度数．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
20、如图，PA，PB分别是⊙O的切线，A，B为切点，AC是⊙O的直径，已知∠BAC=35°，∠P的度数为
如图，PA、PB分别是⊙O的切线，A、B是切点，AC是⊙O的直径．已知∠APB=70°，则∠ACB的度数为
（2012•谷城县模拟）如图，PA、PB是⊙O 的切线，切点分别是A、B，点C是⊙O上异与点A、B的点，如果∠P=60°，那么∠ACB等于
如图，PA、PB是⊙O的切线，切点分别是A、B，若∠APB=60°，PA=4．求⊙O的半径．
如图，PA、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交PA、PB于点E、F，已知PA=12cm，∠P=40°