题目内容
如图，PA、PB分别是⊙O的切线，A、B是切点，AC是⊙O的直径．已知∠APB=70°，则∠ACB的度数为分析：由于PA、PB都是⊙O的切线，由切线长定理知PA=PB，知道了顶角∠APB的度数，即可求得底角∠PBA的度数，进而可由弦切角定理求出∠ACB的度数．
解答：解：∵PA、PB分别是⊙O的切线，
∴PA=PB；
∵∠APB=70°，
∴∠PBA=
（180°-∠APB）=55°，
∵PB切⊙O于B，
∴∠ACB=∠PBA=55°．
∴PA=PB；
∵∠APB=70°，
∴∠PBA=
| 1 |
| 2 |
∵PB切⊙O于B，
∴∠ACB=∠PBA=55°．
点评：此题主要考查了切线长定理和弦切角定理的综合应用能力．
练习册系列答案
相关题目
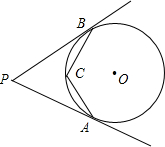如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，已知∠P=50°，则∠ACB=
7、如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=30°，则∠ACB=（ ）
7、如图，PA，PB分别切⊙O于点A，B，点C是AB上一点，过C作⊙O的切线，交PA，PB于点D，E，若PA=6cm，则△PDE的周长是
（2012•绵阳）如图，PA、PB分别切⊙O于A、B，连接PO、AB相交于D，C是⊙O上一点，∠C=60°．
如图，PA，PB分别切⊙O于点A和点B，C是