题目内容
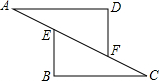如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．试说明DF∥BE．考点：全等三角形的判定与性质
专题：证明题
分析：根据等式的性质就可以求出AF=CE，由平行线的性质就可以得出∠A=∠C．就可以得出△ADF≌△CBE，就有∠AFD=∠CEB，就可以得出结论．
解答：证明：∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE．
∵AD∥BC，
∴∠A=∠C．
在△ADF和△CBE中，
，
∴△ADF≌△CBE（AAS），
∴∠AFD=∠CEB，
∴DF∥BE．
∴AE+EF=CF+EF，
∴AF=CE．
∵AD∥BC，
∴∠A=∠C．
在△ADF和△CBE中，
|
∴△ADF≌△CBE（AAS），
∴∠AFD=∠CEB，
∴DF∥BE．
点评：本题考查了等式的性质的运用，平行线的性质及判定的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．
练习册系列答案
相关题目
某校数学兴趣小组成员高超对本班上期期末考试数学成绩作了统计分析，绘制成如下频数、频率分布表和频数分布直方图．
如图，AC=AD，BC=BD，求证：AB平分∠CAD．
如图，两个同心圆的半径分别为18cm和30cm，又知∠COD=30°，求阴影部分ABDC的面积．