题目内容
1. 如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B.
如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B.(1)求证:AC=BD;
(2)若OA=2,∠A=30°,当AC⊥BD时,求弧$\widehat{CD}$的长.
分析 (1)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,根据圆周角定理得出∠EDB=∠FCA=90°,故可得出△DEB≌△CFA,由此得出结论;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,求出∠COA的度数,再由三角形外角的性质得出∠EOA的度数,由弧长公式即可得出结论.
解答 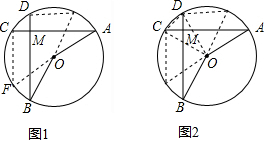 (1)证明:延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,
(1)证明:延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,
∵BE,AF是⊙O的直径,
∴∠EDB=∠FCA=90°.
在△DEB与△CFA中,
∵$\left\{\begin{array}{l}{∠EDB=∠FCA}\\{∠B=∠A}\\{EB=FA}\end{array}\right.$,
∴△DEB≌△CFA(AAS),
∴AC=BD;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,
∵∠A=30°,OA=OC,
∴∠COA=180°-30°-30°=120°.
∵∠A=∠B=30°,AC⊥BD,
∴∠EOA+∠A=60°,
∴∠EOA=30°,
∴∠DOE=60°,
∴∠COD=30°,
∴${l}_{\widehat{CD}}$=$\frac{30πr}{180}$=$\frac{1}{3}$π.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
6.某路口交通信号灯的时间设置为:红灯亮25秒,绿灯亮30秒,黄灯亮5秒.当人或车随意经过该路口时,遇到绿灯的概率为( )
| A. | $\frac{1}{60}$ | B. | $\frac{1}{30}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
13.一个不透明的布袋中装有1个黄球,2个红球和3个白球,这些球除颜色不同外其他完全相同,则从布袋中随机摸出一个球是白球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.如果a与5互为相反数,则|a+2|等于( )
| A. | -3 | B. | 3 | C. | -2 | D. | 2 |
11.若抛物线y=x2+bx+c与x轴有唯一公共点,且过点A(m,n),B(m-8,n),则n=( )
| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
 我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点O为圆心,正方形的对角线OA长为半径画弧.交数轴于点B、C.请根据图形填空.
我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点O为圆心,正方形的对角线OA长为半径画弧.交数轴于点B、C.请根据图形填空.