题目内容
 如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.
如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.考点:三角形中位线定理
专题:证明题
分析:取YZ中点E,连结AE、BE.由A、B分别是YN、MZ的中点,E是YZ的中点,根据三角形中位线定理可得AE∥NZ,AE=
NZ;BE∥MY,BE=
MY;而MY=NZ,等量代换得出BE=AE,根据等边对等角的性质得出∠BAE=∠ABE,再由AE∥NZ,BE∥MY,根据两直线平行,内错角相等得出∠BAE=∠NDC,∠ABE=∠MCD,于是∠NDC=∠MCD,再根据等角对等边即可证明XC=XD.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:取YZ中点E,连结AE、BE.
证明:取YZ中点E,连结AE、BE.
∵A、B分别是YN、MZ的中点,E是YZ的中点,
∴AE∥NZ,AE=
NZ;BE∥MY,BE=
MY;
∵MY=NZ,
∴BE=AE,
∴∠BAE=∠ABE,
∵AE∥NZ,BE∥MY,
∴∠BAE=∠NDC,∠ABE=∠MCD,
∴∠NDC=∠MCD,
∴XC=XD.
 证明:取YZ中点E,连结AE、BE.
证明:取YZ中点E,连结AE、BE.∵A、B分别是YN、MZ的中点,E是YZ的中点,
∴AE∥NZ,AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵MY=NZ,
∴BE=AE,
∴∠BAE=∠ABE,
∵AE∥NZ,BE∥MY,
∴∠BAE=∠NDC,∠ABE=∠MCD,
∴∠NDC=∠MCD,
∴XC=XD.
点评:本题考查了三角形中位线定理,平行线的性质,等腰三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
 游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.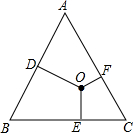 如图三条道路相交围成了一块三角形空地,现要加以绿化,测得AB=BC=AC=115.4米,三角形内的标牌O到三边的距离0F、0D、0E的长度分别为21米、34米、45米,问这块地的面积为多少平方米?
如图三条道路相交围成了一块三角形空地,现要加以绿化,测得AB=BC=AC=115.4米,三角形内的标牌O到三边的距离0F、0D、0E的长度分别为21米、34米、45米,问这块地的面积为多少平方米?