题目内容
 如图,⊙O与正六边形的相邻两边相切,切点分别是D、E,若P是⊙O上异于D、E的任一点,那么∠DPE的度数为
如图,⊙O与正六边形的相邻两边相切,切点分别是D、E,若P是⊙O上异于D、E的任一点,那么∠DPE的度数为30°或150°
30°或150°
.分析:连接OD,OE,由圆O与正六边形相邻两边相切,得到OD与边DA,OE与边EB垂直,再由正六边形的每一个内角为120°,利用四边形的内角和定理求出圆心角∠DOE的度数,利用同弧所对的圆心角等于所对圆周角的2倍即可求出∠DPE的度数.
解答: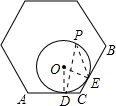 解:连接OD,OE,
解:连接OD,OE,
∵圆与正六边形邻边相切,
∴OD⊥AC,OE⊥BC,
∴∠ODC=∠OEC=90°,
∵正六边形的内角为120°,即∠C=120°,
∴∠DOE=60°,
当P在
上时,如图所示,∠DPE=
∠DOE=30°;
当P在
上时,∠DPE=150°,
综上,∠DPE=30°或150°.
故答案为:30°或150°
 解:连接OD,OE,
解:连接OD,OE,∵圆与正六边形邻边相切,
∴OD⊥AC,OE⊥BC,
∴∠ODC=∠OEC=90°,
∵正六边形的内角为120°,即∠C=120°,
∴∠DOE=60°,
当P在
 |
| DPE |
| 1 |
| 2 |
当P在
 |
| DE |
综上,∠DPE=30°或150°.
故答案为:30°或150°
点评:此题考查了切线的性质,圆周角定理,正六边形的性质,此题答案有两解,注意不要漏解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
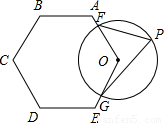
 如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O是正三角形的中心,则四边形OABC的面积等于
如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O是正三角形的中心,则四边形OABC的面积等于 (2012•长春)如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则
(2012•长春)如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则
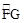 所对的圆周角∠FPG的大小为
度.
所对的圆周角∠FPG的大小为
度.