题目内容
 (2012•长春)如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则
(2012•长春)如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则 | FG |
60
60
度.分析:首先求得正六边形OABCDE的内角的度数,然后由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得答案.
解答:解:∵六边形OABCDE是正六边形,
∴∠AOE=
=120°,
即∠FOG=120°,
∴∠FPG=
∠FOG=60°.
故答案为:60.
∴∠AOE=
| 180°×(6-2) |
| 6 |
即∠FOG=120°,
∴∠FPG=
| 1 |
| 2 |
故答案为:60.
点评:此题考查了圆周角定理与正六边形的性质.此题比较简单,注意掌握正六边形内角的求法与在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用,注意数形结合思想的应用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
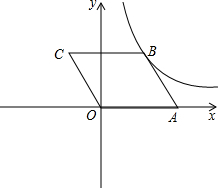 (2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=
(2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=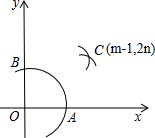 (2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于
(2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于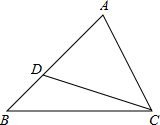 (2012•长春)如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为
(2012•长春)如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为 (2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )
(2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )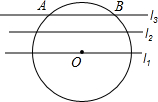 (2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
(2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.