题目内容
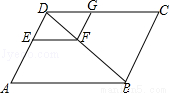
如图,正方形ABCD和正方形CEFG中,D在CG上,BC=1,CG=3,H是AF的中点,则CH的长是 。

 .
.
【解析】
试题分析:连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.
试题解析:如图,连接AC、CF,

∵正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC= ,CF=3
,CF=3 ,
,
∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF= ,
,
∵H是AF的中点,
∴CH= AF=
AF= .
.
考点:1.直角三角形斜边上的中线;2.勾股定理;3.勾股定理的逆定理.

练习册系列答案
相关题目
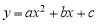 的图象如图所示,则下列关系式不正确的是( )
的图象如图所示,则下列关系式不正确的是( )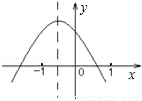
 B.
B. C.
C. D.
D.

 + mx + 2=0的一个根是x=2,则m = 。
+ mx + 2=0的一个根是x=2,则m = 。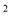 -4x-2=0,变形后为( )
-4x-2=0,变形后为( )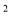 = 6 B、(x-4)
= 6 B、(x-4)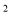 = 6 C、(x-2)
= 6 C、(x-2) 是⊙
是⊙ 的直径,
的直径, ,
, 分别是过⊙
分别是过⊙ 上点
上点 ,
, 的切线,且
的切线,且  .连接
.连接 ,则
,则 的度数是 .
的度数是 .
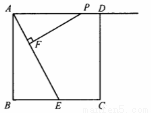
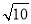 ,求△PFA的面积
,求△PFA的面积