如图.在?ABCD中.EF∥AB.FG∥ED.DE∶EA＝2∶3.EF＝4.求线段CG的长．题目和参考答案——青夏教育精英家教网—

题目内容

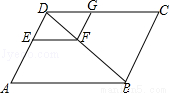
（10分）如图，在?ABCD中，EF∥AB，FG∥ED，DE∶EA＝2∶3，EF＝4，求线段CG的长．

6．

【解析】

试题分析：首先借助相似三角形的判定及其性质求出AB的长度，然后证明DG=EF，问题即可解决．

试题解析：∵EF∥AB，∴△DEF∽△DAB，∴，∵，∴，而EF=4，∴AB=10；∵四边形ABCD是平行四边形，∴DC=AB=10；∵FG∥ED，∴△DGF∽△DCB，∴，

∴，∵DC=AB，∴DG=EF=4，GC=10﹣4=6，即线段CG的长为6．

考点：1．平行四边形的判定与性质；2．平行线分线段成比例．

练习册系列答案

单元考王系列答案

相关题目

写出两个你熟悉的中心对称的几何图形名称，它是

如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）．

（1）求此抛物线的解析式

（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明；

（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为（）

A．30° B．60° C．90° D．150°

下列命题中正确的是（）

A．对角线相等的四边形是矩形

B．对角线互相垂直的四边形是菱形

C．对角线互相垂直平分且相等的四边形是正方形

D．一组对边相等，另一组对边平行的四边形是平行四边形

如果函数是二次函数，那么k的值一定是 .

如图：DE是△ABC的中位线，延长DE至F使EF＝DE，连接CF，则S△CEF∶S四边形BCED的值为（）

A．1∶3 B．2∶3 C．1∶4 D．2∶5

如图，正方形ABCD和正方形CEFG中，D在CG上，BC=1，CG=3，H是AF的中点，则CH的长是。

为了落实国家的惠农政策，某地政府制定了农户投资购买收割机的补贴办法，其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系：

（1）分别求出y1和y2的函数表达式；

试题分类