题目内容
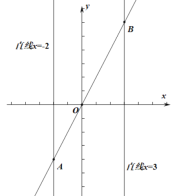
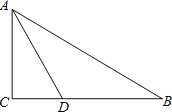
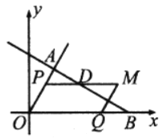
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 、
、![]() 分别是射线
分别是射线![]() 、线段
、线段![]() 上的点,且
上的点,且![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,①若线段
,①若线段![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,则
时,则![]() _______;②把
_______;②把![]() 沿着
沿着![]() 进行折叠,当折叠后
进行折叠,当折叠后![]() 与
与![]() 的重叠部分的面积是平行四边形
的重叠部分的面积是平行四边形![]() 的
的![]() 时,则
时,则![]() _______.
_______.
【答案】![]()
![]() 或
或![]()
【解析】
①根据![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,四边形
,四边形![]() 平行四边形,得到
平行四边形,得到![]() ,
,![]() ,
,![]() 设
设![]() ,则由
,则由![]() 得
得![]() ,
,![]() ,则利用
,则利用![]() ,
,![]() , 即可得
, 即可得![]() ,即可得出结果;
,即可得出结果;
②分两种情况讨论(1)当![]() 点在线段
点在线段![]() 之间时,(2)当
之间时,(2)当![]() 点在射线
点在射线![]() 上时,分别进行求解即可.
上时,分别进行求解即可.
解:①∵![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵四边形![]() 平行四边形,
平行四边形,
∴![]() ,
,
∴![]()
设![]() ,则由
,则由![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
则有:![]() ①,
①,
![]() ②,
②,
即可得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
②把![]() 沿着
沿着![]() 进行折叠,折叠后得图形是
进行折叠,折叠后得图形是![]()
(1)如图示,当![]() 点在线段
点在线段![]() 之间时,
之间时,![]() 交
交![]() 于
于![]() 点,
点,
∵折叠后![]() 与
与![]() 的重叠部分的面积是平行四边形
的重叠部分的面积是平行四边形![]() 的
的![]() ,
,
即![]() ,
,
∴![]()
即![]() 把
把![]() 分成了面积相等得两部分,
分成了面积相等得两部分,
∴![]() 是
是![]() 的中线,
的中线,
∴![]()
又∵四边形![]() 平行四边形,
平行四边形,![]() ,
,
∴![]() ,
,
∵折叠![]() 得到
得到 ![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 是等腰三角形,
是等腰三角形,
∴![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
即有![]() ,
,
∴![]() ,
,
∴![]() ;
;
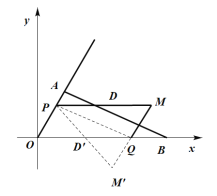
(2)如图示,当![]() 点在射线
点在射线![]() 上时,
上时,![]() 交
交![]() 于
于![]() 点,
点,

∵折叠后![]() 与
与![]() 的重叠部分的面积是平行四边形
的重叠部分的面积是平行四边形![]() 的
的![]() ,
,
即![]() ,
,
∴![]()
即![]() 把
把![]() 分成了面积相等得两部分,
分成了面积相等得两部分,
∴![]() 是
是![]() 的中线,
的中线,
∴![]() ,
,
又∵四边形![]() 平行四边形,
平行四边形,![]() ,
,
∴![]() ,
,
∵折叠![]() 得到
得到 ![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 是等腰三角形,
是等腰三角形,
∴![]()
∴![]()
∴![]() 是等边三角形,
是等边三角形,
∴![]()
即有![]() ,
,
∴![]()
∴![]() .
.

练习册系列答案
相关题目