题目内容
3.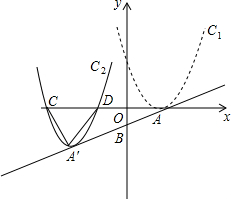 如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )
如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
分析 设抛物线C2的顶点A′坐标是(a,b),根据抛物线的对称性质和一次函数图象上点的坐标特征来求点A′的坐标,则易求AA′的长度.
解答 解:∵抛物线C1的解析式为y=(x-2)2,
∴其顶点A的坐标是(2,0).
抛物线C2的顶点A′坐标是(a,b)(b<0).
则抛物线C2的解析式为y=(x-a)2+b=x2-2ax+a2+b.
∴CD=$\sqrt{(-2a)^{2}-4({a}^{2}+b)}$.
又∵△A′CD为正三角形,
∴A′C=CD=$\sqrt{(-2a)^{2}-4({a}^{2}+b)}$.
依题意得 $\left\{\begin{array}{l}{b=\frac{1}{2}a-1}\\{b=-\frac{\sqrt{3}}{2}\sqrt{(-2a)^{2}-4({a}^{2}+b)}}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-4}\\{b=-3}\end{array}\right.$.
∴A′(-4,-3).
∴AA′=$\sqrt{(-4-2)^{2}+(-3)^{2}}$=3$\sqrt{5}$.
故选:B.
点评 本题考查了二次函数图象与几何变换.解题的难点是根据△A′CD为正三角形来求点A′的纵坐标与边CD的数量关系.

练习册系列答案
相关题目
3.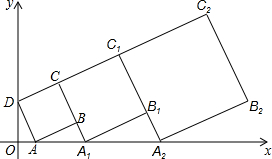 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )| A. | 5($\frac{3}{2}$)2010 | B. | 5($\frac{9}{4}$)2010 | C. | 5($\frac{9}{4}$)2011 | D. | 5($\frac{3}{2}$)2011 |
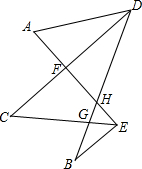 如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.
如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.