题目内容
15. 如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(-1,5),B(-3,0),C(-4,3).
如图所示,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(-1,5),B(-3,0),C(-4,3).(1)画出把△ABC向右平移6个单位,再向上平移1个单位长度的三角形A′B′C′;
(2)写出平移后三角形A′B′C′的各顶点的坐标;
(3)求三角形A′B′C′的面积.
分析 (1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)利用△A′B′C′所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
解答  解:(1)△A′B′C′如图所示;
解:(1)△A′B′C′如图所示;
(2)A′(5,6),B′(3,1),C′(2,4);
(3)△A′B′C′的面积=3×5-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×5-$\frac{1}{2}$×2×3,
=15-1.5-5-3,
=15-9.5,
=4.5.
点评 本题考查了利用平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
5.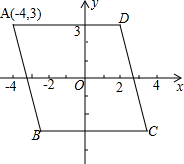 如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
 如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )| A. | (4,-3) | B. | (3,-4) | C. | (4,-4) | D. | (3,-3) |
10.下列命题中的假命题是( )
| A. | 同位角一定相等 | B. | 平移不改变图形的形状和大小 | ||
| C. | 无理数是无限不循环小数 | D. | 点M(a,-a)可能在第二象限 |
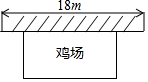 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m,鸡场的面积能达到180m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m,鸡场的面积能达到180m2吗?如果能,请你给出设计方案;如果不能,请说明理由.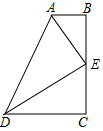 如图,四边形ABCD中,AB∥CD,∠B=∠C=90°,E是BC边上的中点,AE平分∠DAB,∠ADE=30°,下面有五个结论:
如图,四边形ABCD中,AB∥CD,∠B=∠C=90°,E是BC边上的中点,AE平分∠DAB,∠ADE=30°,下面有五个结论: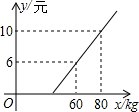 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):
某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):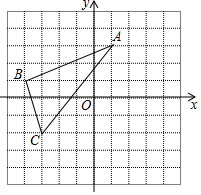 如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).
如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).