题目内容
三角形三边长a、b、c满足a2(b-c)+b2c-b3=0,则这个三角形的形状是( )
分析:先把等式分解为(a+b)(a-b)(b-c)=0的形式,进而可判断出△ABC的形状.
解答:解:原方程可化为:(a+b)(a-b)(b-c)=0,
∴a=b或b=c,
∴此三角形是等腰三角形.
故选A.
∴a=b或b=c,
∴此三角形是等腰三角形.
故选A.
点评:本题考查的是因式分解的应用,此题易把等式分解成(a2-b2)(b-c)=0的形式而造成因式分解不彻底.

练习册系列答案
相关题目
下列能构成直角三角形三边长的是( )
| A、2,3,4 | ||
| B、2,2,3 | ||
C、
| ||
| D、2,6,5 |
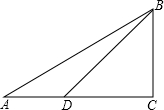 如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.
如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.