��Ŀ����
7��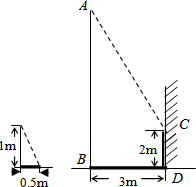 ��ͼ��ijһʱ�̣�С����ֱ��������һ��1m�ߵ�ֱ�ˣ��������������µ�Ӱ��Ϊ0.5m����ʱ���Ա�һ���߸�AB�������µ�Ӱ�ӷֱ������˵��Ϻ�ǽ�ϣ��������õ��߸�AB���ڵ����ϵ�Ӱ�Ӳ���BD��Ϊ3m������ǽ�ϵ�Ӱ�Ӳ���CD��Ϊ2m��С������Щ���ݺܿ�����˵��߸�AB�ĸߣ��������һ�£�
��ͼ��ijһʱ�̣�С����ֱ��������һ��1m�ߵ�ֱ�ˣ��������������µ�Ӱ��Ϊ0.5m����ʱ���Ա�һ���߸�AB�������µ�Ӱ�ӷֱ������˵��Ϻ�ǽ�ϣ��������õ��߸�AB���ڵ����ϵ�Ӱ�Ӳ���BD��Ϊ3m������ǽ�ϵ�Ӱ�Ӳ���CD��Ϊ2m��С������Щ���ݺܿ�����˵��߸�AB�ĸߣ��������һ�£���1�����߸�AB�ĸ�Ϊ���٣�
��2��С����Ϊ���ڵ��Ϻ�ǽ�ϵ�Ӱ�ӳ���Ӿ��ǵ��߸�Ӱ��ȫ�����ڵ�����ʱ��Ӱ��������Ϊ���������ԣ���������߸�ABӰ��ȫ�����ڵ�����ʱ��Ӱ����
���� ��1��������ͬһʱ�̡�ͬһ�ص�����ĸ�����Ӱ�ӳ��ı�ֵ��ͬ�����
��2������߸�ABӰ��ȫ�����ڵ�����ʱ��Ӱ��Ϊx�ף����ݡ������ʵ�ʸ߶Ⱥ�Ӱ���ɱ������г����̲����
���  ��1���⣺����C��CE��BD����AB�ڵ�E�����ı���CEBDΪ���Σ�
��1���⣺����C��CE��BD����AB�ڵ�E�����ı���CEBDΪ���Σ�
��CE=BD=3��EB=CD=2��
�������� $\frac{AE}{EC}=\frac{1}{0.5}$���� $\frac{AE}{3}=\frac{1}{0.5}$��
��AE=6��
��AB=AE+EB=6+2=8��
�����߸�AB�ĸ�Ϊ8�ף�
��2�����ԣ��������£�
����߸�ABӰ��ȫ�����ڵ�����ʱ��Ӱ��Ϊx�ף���$\frac{8}{x}=\frac{1}{0.5}$��
��x=4���ף�
�𣺵��߸�ABӰ��ȫ�����ڵ�����ʱ��Ӱ��Ϊ4�ף�
���� ����ֻҪ�ǰ�ʵ��������������������У��������������ε����Ʊȣ��г���ʽ����⼴�ɣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
17�����и�ʽ�������θ�ʽ���ǣ�������
| A�� | $\sqrt{0.3}$ | B�� | $\sqrt{{a}^{2}-{b}^{2}}$ | C�� | $\sqrt{{a}^{2}b}$ | D�� | $\sqrt{12}$ |
15�������ж���ʽ�˷��У�������ƽ���ʽ������ǣ�������
| A�� | ��a-b����-a+b�� | B�� | ��m3-n3����m3+n3�� | C�� | ��-7-x����7-x�� | D�� | ��x2-y2����y2+x2�� |
 ��ͼ��E���ı���ADBC�ڵ�һ�㣬����AE��CE��DE��AB�����$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$����ADB���AEC������Ϊʲô��
��ͼ��E���ı���ADBC�ڵ�һ�㣬����AE��CE��DE��AB�����$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$����ADB���AEC������Ϊʲô��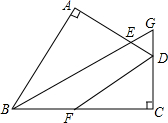 ��ͼ���ı���ABCD�У���A=��C=90�㣬BEƽ�֡�ABC��DFƽ�֡�ADC��BE��CD����G��
��ͼ���ı���ABCD�У���A=��C=90�㣬BEƽ�֡�ABC��DFƽ�֡�ADC��BE��CD����G�� һ��������ľ����������Ϸֱ�д������1��2��3��4��5��6���������ͼ��ͼ��ʾ����д4�������Ķ���д��3��
һ��������ľ����������Ϸֱ�д������1��2��3��4��5��6���������ͼ��ͼ��ʾ����д4�������Ķ���д��3��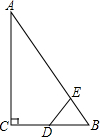 ��ͼ����Rt��ABC�У���ACB=90�㣬��ABC=60�㣬BC=2cm����DΪBC���е㣬����E�ӵ�A����������A��B��A�ķ�����1cm/s���ٶ��˶������ص���Aʱֹͣ�˶�������DE�����E���˶�ʱ��Ϊt��s������BDE�����ΪS��cm2��������涨���߶������Ϊ0�ļ���ͼ�Σ���
��ͼ����Rt��ABC�У���ACB=90�㣬��ABC=60�㣬BC=2cm����DΪBC���е㣬����E�ӵ�A����������A��B��A�ķ�����1cm/s���ٶ��˶������ص���Aʱֹͣ�˶�������DE�����E���˶�ʱ��Ϊt��s������BDE�����ΪS��cm2��������涨���߶������Ϊ0�ļ���ͼ�Σ���