题目内容
若双曲线y=
经过点P(a,b),且a、b是方程x2-4x-6=0的两根.则k=
| k | x |
-6
-6
.分析:先求出方程x2-4x-6=0的两根,再根据双曲线y=
经过点P(a,b)即可求出k的值.
| k |
| x |
解答:解:解方程x2-4x-6=0得,x1=2+
,x2=2-
,
∵a、b是方程x2-4x-6=0的两根,
∴令a=2+
,b=2-
,
∵双曲线y=
经过点P(a,b),
∴k=ab=(2+
)(2-
)=-6.
故答案为:-6.
| 10 |
| 10 |
∵a、b是方程x2-4x-6=0的两根,
∴令a=2+
| 10 |
| 10 |
∵双曲线y=
| k |
| x |
∴k=ab=(2+
| 10 |
| 10 |
故答案为:-6.
点评:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.

练习册系列答案
相关题目
 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线 如图,正方形OBCD的边长为2,点E是BC上的中点,点F是边OD上一点,若双曲线y=
如图,正方形OBCD的边长为2,点E是BC上的中点,点F是边OD上一点,若双曲线y=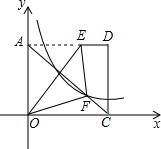 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=