题目内容
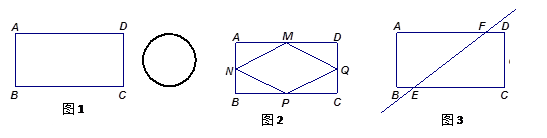
如图1, 矩形铁片ABCD中,AD=8, AB=4; 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
(1)直接写出矩形铁片ABCD的面积 ;
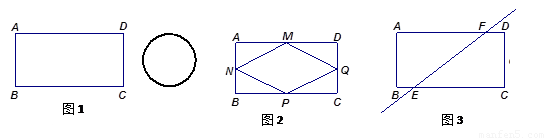
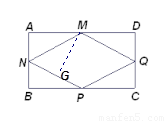
(2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
① 证明四边形MNPQ是菱形;
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.
(1) 32
(2)① 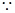 M、N、P、Q分别是AD、AB、BC、CD的中点,MN=NP=PQ=QM=
M、N、P、Q分别是AD、AB、BC、CD的中点,MN=NP=PQ=QM=
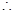 四边形MNPQ是菱形
四边形MNPQ是菱形
② 如图,过点M作MG⊥NP于点G
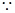
 =16
=16 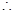 MG=
MG=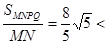 3.8
3.8
 此时铁片能穿过圆孔
此时铁片能穿过圆孔
(3) 如图,过点A作AH⊥EF于点H, 过点E作EK⊥AD于点K 显然AB=4>3.8,
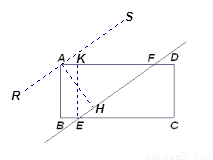
故沿着与AB垂直的方向无法穿过圆孔
过点A作EF的平行线RS,故只需计算直线RS与EF之间的距离即可
 BE=AK=1,
EK=AB=4,AF=7
BE=AK=1,
EK=AB=4,AF=7
 KF=6, EF=
KF=6, EF=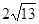
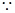 ∠AHF=∠EKF=90°,∠AFH=∠EFK
∠AHF=∠EKF=90°,∠AFH=∠EFK
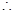 △AHF∽△EKF
△AHF∽△EKF
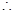
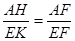 可得AH=
可得AH=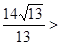 3.8
直角梯形铁片不能穿过圆孔
3.8
直角梯形铁片不能穿过圆孔
【解析】(1)根据矩形的面积公式:长×宽=面积求出即可;
(2)①利用四条边相等的四边形为矩形来判定四边形为菱形,
②利用面积相等来求得菱形一边的高,与已知数据比较后判断是否能通过.
(2)利用两三角形相似得到比例线段,进而求出点A到EF的距离,然后与已知线段比较,从而判定能否
通过.

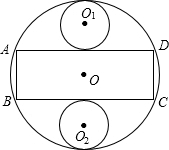 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.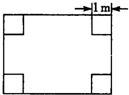 100、张大爷从市场上买回一块矩形铁片,将铁片的四个角各剪出一个边长为1米的正方形,如图所示,剩下的部分刚好能围成一个容积为8米3的无盖长方体且此长方体运输箱底面的长比宽多2米,问张大爷应购买多大的铁皮?
100、张大爷从市场上买回一块矩形铁片,将铁片的四个角各剪出一个边长为1米的正方形,如图所示,剩下的部分刚好能围成一个容积为8米3的无盖长方体且此长方体运输箱底面的长比宽多2米,问张大爷应购买多大的铁皮?