题目内容
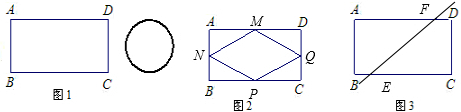
如图1,矩形铁片ABCD中,AD=8,AB=4; 为了要让铁片能穿过直径为3.8的圆孔,需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
(1)直接写出矩形铁片ABCD的面积
(2)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
①证明四边形MNPQ是菱形;
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由.
(1)直接写出矩形铁片ABCD的面积
32
32
;(2)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
①证明四边形MNPQ是菱形;
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由.

分析:(1)根据矩形的面积公式:长×宽=面积求出即可;
(2)①利用四条边相等的四边形为矩形来判定四边形为菱形,
②利用面积相等来求得菱形一边的高,与已知数据比较后判断是否能通过.
(3)利用两三角形相似得到比例线段,进而求出点A到EF的距离,然后与已知线段比较,从而判定能否通过.
(2)①利用四条边相等的四边形为矩形来判定四边形为菱形,
②利用面积相等来求得菱形一边的高,与已知数据比较后判断是否能通过.
(3)利用两三角形相似得到比例线段,进而求出点A到EF的距离,然后与已知线段比较,从而判定能否通过.
解答:解:(1)8×4=32;
(2)①∵M、N、P、Q分别是AD、AB、BC、CD的中点,
MN=NP=PQ=QM=2
,
∴四边形MNPQ是菱形;
②如图,过点M作MG⊥NP于点G,
∵SMNPQ=16,
∴MG=
=
<3.8,
∴此时铁片能穿过圆孔;
(3)如图,过点A作AH⊥EF于点H,过点E作EK⊥AD于点K,
显然AB=4>3.8,
故沿着与AB垂直的方向无法穿过圆孔,
过点A作EF的平行线RS,故只需计算直线RS与EF之间的距离即可,
∵BE=AK=1,EK=AB=4,AF=7,
∴KF=6,EF=2
,
∵∠AHF=∠EKF=90°,∠AFH=∠EFK,
∴△AHF∽△EKF,
∴
=
可得AH=
>3.8,
∴此时铁片不能穿过圆孔.
(2)①∵M、N、P、Q分别是AD、AB、BC、CD的中点,
MN=NP=PQ=QM=2
| 5 |
∴四边形MNPQ是菱形;

②如图,过点M作MG⊥NP于点G,
∵SMNPQ=16,
∴MG=
| SMNPQ |
| MN |
| 8 |
| 5 |
| 5 |
∴此时铁片能穿过圆孔;
(3)如图,过点A作AH⊥EF于点H,过点E作EK⊥AD于点K,
显然AB=4>3.8,

故沿着与AB垂直的方向无法穿过圆孔,
过点A作EF的平行线RS,故只需计算直线RS与EF之间的距离即可,
∵BE=AK=1,EK=AB=4,AF=7,
∴KF=6,EF=2
| 13 |
∵∠AHF=∠EKF=90°,∠AFH=∠EFK,
∴△AHF∽△EKF,
∴
| AH |
| EK |
| AF |
| EF |
可得AH=
14
| ||
| 13 |
∴此时铁片不能穿过圆孔.
点评:此题主要考查了矩形面积求法以及菱形判定和相似三角形的判定与性质,根据已知得出△AHF∽△EKF,进而得出AH的长是解题关键.

练习册系列答案
相关题目
 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);


 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;  的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);


 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由; 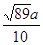 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);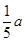 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;