题目内容
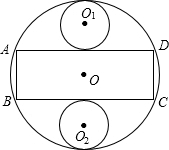 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.(1)若把BC作为油桶的高时,则油桶的底面半径R1等于多少?
(2)当把AB作为油桶的高时,油桶的底面半径R2与(1)中的R1相等吗?若相等,请说明理由;若不相等,请求出R2.
分析:本题的切入口是通过圆柱的侧面展开图--矩形的一条边长等于底面周长和大圆直径等于两个小圆直径加上AB的长,建立半径R1和R2的方程,即2-4R1=2πR1,12=(1-2R2)2+(πR2)2.
解答:解:(1)根据题意,得
2R1+2R1+AB=2,
即2-4R1=2πR1,
∴R1=
≈0.1945(m).
(2)R2与(1)中的R1不相等.
连接OB、OO2.根据题意,得
OB2=(
BC)2+(
AB)2,BC=2πR2,
∴12=(1-2R2)2+(πR2)2,
即R2=
≈0.2884(m).
2R1+2R1+AB=2,
即2-4R1=2πR1,
∴R1=
| 1 |
| π+2 |
(2)R2与(1)中的R1不相等.
连接OB、OO2.根据题意,得
OB2=(
| 1 |
| 2 |
| 1 |
| 2 |
∴12=(1-2R2)2+(πR2)2,
即R2=
| 4 |
| π2+4 |
点评:考查学生经历“问题情境--建立模型--求解--解释与应用”的基本过程,考查学生“用数学,做数学”的意识以及创新精神和实践能力.

练习册系列答案
相关题目
 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.