题目内容
如图,矩形纸片ABCD中,AB=5cm,BC=10cm,CD上有一点E,EC=2cm,AD上有一点P,PA=6cm,过点P作PF⊥AD交BC于点F,将纸片折叠,使P与E重合,折痕交PF于Q,则线段PQ的长是 cm.

 解:连接EQ,
解:连接EQ,
∵将纸片折叠,使P与E重合,
∴△PEQ是等腰三角形,OQ是PE的垂直平分线,
∵矩形纸片ABCD中,AB=5cm,BC=10cm,PA=6cm,CE=2cm,
∴PD=4cm,DE=3cm,
∵在Rt△DPE中PE= =
= =5.
=5.
∴OP= PE=
PE= ,
,
设PQ=x,则QF=5﹣x,
∴OQ= =
=
∵S△PEQ+S梯形QFCE=S梯形PFCE,即: PE•OQ+
PE•OQ+ (
( QF+CE)×CF=
QF+CE)×CF= (PF+CE)×CF,
(PF+CE)×CF,
即 ×5×
×5× +
+ ×(5﹣x+2)×4=
×(5﹣x+2)×4= ×(5+2)×4,
×(5+2)×4,
解得x= cm.
cm.
故答案为: .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目

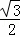 D. 60,
D. 60,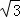

 <﹣
<﹣ C. ﹣2a<﹣2b D. ﹣5+a<﹣5+b
C. ﹣2a<﹣2b D. ﹣5+a<﹣5+b
 有解,则a的取值范围是( )
有解,则a的取值范围是( )