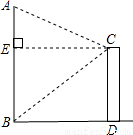
题目内容
如图，某人站在楼顶观测对面笔直的旗杆AB，CE=8米，测得旗杆顶的仰角∠ECA=30°，旗杆底部的俯角∠ECB=45°，那么旗杆AB的高度是
- A.（8
+8
）米 - B.（8+8）米
- C.（8+
）米 - D.（8+）米
D
分析：利用∠ECA的正切值可求得AE；利用∠ECB的正切值可求得BE．AB=AE+BE．
解答：AB=AE+BE=8tan30°+8tan45°=（+8）米．故选D．
点评：本题考查仰角、俯角的概念，以及解直角三角形方法．
分析：利用∠ECA的正切值可求得AE；利用∠ECB的正切值可求得BE．AB=AE+BE．
解答：AB=AE+BE=8tan30°+8tan45°=（
+8）米．故选D．点评：本题考查仰角、俯角的概念，以及解直角三角形方法．
练习册系列答案
相关题目
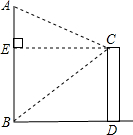如图，某人站在楼顶观测对面笔直的旗杆AB，已知观测点C到旗杆的距离（CE的长度）为8米，测得旗杆顶的仰角为∠ECA=30°，旗杆底部的俯角∠ECB=45°，那么旗杆AB的高度是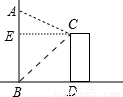
如图，某人站在楼顶观测对面笔直的旗杆AB，CE=8米，测得旗杆顶的仰角∠ECA=30°，旗杆底部的俯角∠ECB=45°，那么旗杆AB的高度是（ ）A、（8
| ||||||
B、（8+8
| ||||||
C、（8
| ||||||
D、（8+
|
+8
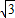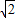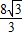）米
）米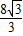
+
）米
）米
