题目内容
8.已知正数x满足x10+x5+$\frac{1}{{x}^{5}}$+$\frac{1}{{x}^{10}}$=15250,则x+$\frac{1}{x}$的值为3.分析 可令x5+$\frac{1}{{x}^{5}}$=m,则x10+x5+$\frac{1}{{x}^{5}}$+$\frac{1}{{x}^{10}}$=15250变形为(x5+$\frac{1}{{x}^{5}}$)2+(x5+$\frac{1}{{x}^{5}}$)-15252=0,得到m2+m-15252=0,解得m,再令x+$\frac{1}{x}$=a,得到x5+$\frac{1}{{x}^{5}}$=(x4+$\frac{1}{{x}^{4}}$)(x+$\frac{1}{x}$)-(x3+$\frac{1}{{x}^{3}}$)=a(a4-4a2+2)-(a3-3a)=a5-5a3+5a,得到a5-5a3+5a=123,再根据公因式法解方程即可求解.
解答 解:令x5+$\frac{1}{{x}^{5}}$=m,
则x10+x5+$\frac{1}{{x}^{5}}$+$\frac{1}{{x}^{10}}$=15250变形为(x10+$\frac{1}{{x}^{10}}$)+(x5+$\frac{1}{{x}^{5}}$)-15250=0,
(x5+$\frac{1}{{x}^{5}}$)2+(x5+$\frac{1}{{x}^{5}}$)-15252=0,
即m2+m-15252=0,
(m-123)(m+124)=0,
解得m1=123,m2=-124,
∵x为正数,
∴m2=-124不合题意舍去,
∴m=123,
令x+$\frac{1}{x}$=a,
则x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=a2-2,
x3+$\frac{1}{{x}^{3}}$=(x2+$\frac{1}{{x}^{2}}$)(x+$\frac{1}{x}$)-(x+$\frac{1}{x}$)=a(a2-2)-a=a3-3a,
x4+$\frac{1}{{x}^{4}}$=(x2+$\frac{1}{{x}^{2}}$)2-2=(a2-2)2-2=a4-4a2+2,
x5+$\frac{1}{{x}^{5}}$=(x4+$\frac{1}{{x}^{4}}$)(x+$\frac{1}{x}$)-(x3+$\frac{1}{{x}^{3}}$)=a(a4-4a2+2)-(a3-3a)=a5-5a3+5a,
∴a5-5a3+5a=123,
(a5-3a4)+3(a4-3a3)+4(a3-3a2)+12(a2-3a)+41(a-3)=0,
(a-3)(a4+3a3+4a2+12a+41)=0,
∴a-3=0,
解得a=3,
即x+$\frac{1}{x}$的值为3.
故答案为:3.
点评 考查了换元法解分式方程,利用完全平方公式以及提取公因式法进行分解得出是解题的关键.换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.

 精英口算卡系列答案
精英口算卡系列答案| A. | 最大的负整数为-1 | B. | 最小的正整数为1 | ||
| C. | 最小的整数是0 | D. | 相反数等于它本身的数是0 |
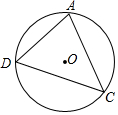 如图,△ADC内接于⊙O.
如图,△ADC内接于⊙O. 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为1.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为1.