题目内容
甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为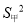 =16.7,乙比赛成绩的方差为
=16.7,乙比赛成绩的方差为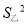 =28.3,那么成绩比较稳定的是___(填“甲”或“乙”).
=28.3,那么成绩比较稳定的是___(填“甲”或“乙”).
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为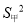 =16.7,乙比赛成绩的方差为
=16.7,乙比赛成绩的方差为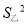 =28.3,那么成绩比较稳定的是___(填“甲”或“乙”).
=28.3,那么成绩比较稳定的是___(填“甲”或“乙”).
 期末集结号系列答案
期末集结号系列答案