题目内容
已知:如图,∠ACB=90°,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,连OE交DC于P,则下列结论,其中正确的有( )①BC=2DE; ②OE∥AB; ③DE=
 PD; ④AC•DF=DE•CD.
PD; ④AC•DF=DE•CD.
A.①②③
B.①③④
C.①②④
D.①②③④
【答案】分析:本题是一道利用切线性质解答的有关圆的知识题目,根据已知条件可以对已有的4个结论一一进行求解证明,利用切线长定理可以得到P为中点,利用三角形的中位线得到平行,得到E为中点,得到相应答案,利用三角形相似得到④AC•DF=DE•CD,从而得出答案.
解答: 解:∵∠ACB=90°
解:∵∠ACB=90°
∴BC是⊙O的切线
∵BC是⊙O的切线
∴OE垂直平分CD,∠OEC=∠ODE
∴P是CD的中点
∴OP∥AB,
∴OE∥AB
②正确,
∴E是BC的中点
∵AC是直径
∴∠ADC=90°
∴CD⊥AB
∴∠CDB=90°
∴BC=2DE,①正确;
∵EF⊥AB
∴∠DFE=90°
∴△ACD∽△EDF
∴
∴AC•DF=DE•CD,④正确.
在四边形PDFE中,我们可以证明它是矩形,而不具备证明它是正方形的条件,
∴DE= 只有PE=PD时DE才等于
只有PE=PD时DE才等于 PD.
PD.
∴③DE= PD不成立
PD不成立
综上所述,正确的是C
故选C
点评:本题考查了圆的切线的性质、圆周角定理,相似三角形的判定与性质,切线长性质及三角形的中位线的运用
解答:
 解:∵∠ACB=90°
解:∵∠ACB=90°∴BC是⊙O的切线
∵BC是⊙O的切线
∴OE垂直平分CD,∠OEC=∠ODE
∴P是CD的中点
∴OP∥AB,
∴OE∥AB
②正确,
∴E是BC的中点
∵AC是直径
∴∠ADC=90°
∴CD⊥AB
∴∠CDB=90°
∴BC=2DE,①正确;
∵EF⊥AB
∴∠DFE=90°
∴△ACD∽△EDF
∴

∴AC•DF=DE•CD,④正确.
在四边形PDFE中,我们可以证明它是矩形,而不具备证明它是正方形的条件,
∴DE=
 只有PE=PD时DE才等于
只有PE=PD时DE才等于 PD.
PD.∴③DE=
 PD不成立
PD不成立综上所述,正确的是C
故选C
点评:本题考查了圆的切线的性质、圆周角定理,相似三角形的判定与性质,切线长性质及三角形的中位线的运用

练习册系列答案
相关题目
 14、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是
14、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是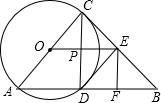 已知:如图,∠ACB=90°,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,连OE交DC于P,则下列结论,其中正确的有( )
已知:如图,∠ACB=90°,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,连OE交DC于P,则下列结论,其中正确的有( ) 36、已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F,
36、已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F, 已知:如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上.
已知:如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上.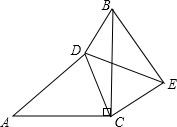 已知:如图,∠ACB=90°,AC=BC,AD=BE,∠CAD=∠CBE.
已知:如图,∠ACB=90°,AC=BC,AD=BE,∠CAD=∠CBE.