题目内容
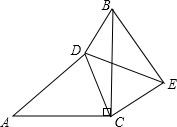 已知:如图,∠ACB=90°,AC=BC,AD=BE,∠CAD=∠CBE.
已知:如图,∠ACB=90°,AC=BC,AD=BE,∠CAD=∠CBE.(1)判断△DCE的形状,并说明你的理由;
(2)当BD:CD=1:2时,∠BDC=135°时,求sin∠BED的值.
分析:(1)根据全等三角形的证明及性质即可得出结论;
(2)根据等腰直角三角形的性质及锐角正弦值即可得出答案.
(2)根据等腰直角三角形的性质及锐角正弦值即可得出答案.
解答:证明:(1)∵AC=BC,AD=BE,∠CAD=∠CBE,
∴△ADC≌△BEC
∴DC=EC,∠1=∠2.
∵∠1+∠BCD=90°,
∴∠2+∠BCD=90°.
∴△DCE是等腰直角三角形;

解:(2)∵△DCE是等腰直角三角形.
∴∠CDE=45°.
∵∠BDC=135°,
∴∠BDE=90°
∵BD:CD=1:2,
设BD=x,则CD=2x,DE=2
x,BE=3x.
∴sin∠BED=
=
.
∴△ADC≌△BEC
∴DC=EC,∠1=∠2.
∵∠1+∠BCD=90°,
∴∠2+∠BCD=90°.
∴△DCE是等腰直角三角形;

解:(2)∵△DCE是等腰直角三角形.
∴∠CDE=45°.
∵∠BDC=135°,
∴∠BDE=90°
∵BD:CD=1:2,
设BD=x,则CD=2x,DE=2
| 2 |
∴sin∠BED=
| BD |
| BE |
| 1 |
| 3 |
点评:本题主要考查了全等三角形的证明及性质,同时考查了等腰直角三角形的性质及锐角三角函数表达式,难度适中.

练习册系列答案
相关题目
 14、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是
14、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是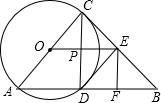 已知:如图,∠ACB=90°,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,连OE交DC于P,则下列结论,其中正确的有( )
已知:如图,∠ACB=90°,以AC为直径的⊙O交AB于D点,过D作⊙O的切线交BC于E点,EF⊥AB于F点,连OE交DC于P,则下列结论,其中正确的有( ) 36、已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F,
36、已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F, 已知:如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上.
已知:如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上.