题目内容
11.已知:在△ABC和△DEF中,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.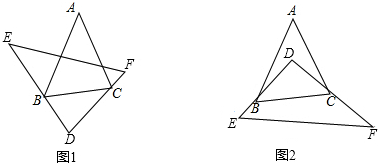
(1)当将△DEF如图1摆放时,若∠A=50°,∠E+∠F=100°,则∠ABD+∠ACD=230度.
(2)当将△DEF如图2摆放时,∠A=m°,∠E+∠F=n°,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论不能(填“能”或“不能”)
分析 (1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-50°=130°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°,得出∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°;
(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB-(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=n°;根据三角形内角和定理得,∠ABC+∠ACB=180°-∠A=(180-m)°,得出∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=(180-m-n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
解答 解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=50°
∴∠ABC+∠ACB=180°-50°=130°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°-∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°-∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°.
(2)∠ABD+∠ACD=(180-m-n)°;
理由如下:
∵∠E+∠F=n°
∴∠CBD+∠BCD=∠E+∠F=n°
∴∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=(180-m-n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
点评 此题考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.

| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
| A. | -2 | B. | ±2 | C. | 2 | D. | 16 |
| A. | AC=BD | B. | AC⊥BD | C. | AO=DO | D. | AO=CO |
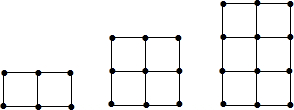
(1)搭一搭,填一填:
| 第几个图形 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | 7 | 12 | 17 | 22 | … |
 如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是4.
如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是4.