题目内容
20. 在矩形ABCD中,对角线AC,BD相交于O点,∠AOB=60°,AE平分∠BAD交BC于E
在矩形ABCD中,对角线AC,BD相交于O点,∠AOB=60°,AE平分∠BAD交BC于E(1)求证:△AOB是等边三角形;
(2)求证:AC=2BE;
(3)求∠COE的度数.
分析 (1)由矩形的性质得出OA=OB,再由∠AOB=60°,即可得出结论;
(2)由矩形的性质和角平分线得出△ABE是等腰直角三角形,得出BE=AB=OA,即可得出结论;
(3)由矩形的性质和(1)的结论得出∠OBE=30°,证出OB=BE,求出∠BOE,即可得出∠COE的度数.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABD=90°,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
又∵∠AOB=60°,
∴△AOB是等边三角形;
(2)证明:由(1)得:△AOB是等边三角形,
∴AB=OB=OA=$\frac{1}{2}$AC,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴BE=AB,
∴BE=OA,
∴AC=2BE;
(3)解:由(1)得:△AOB是等边三角形,
∴∠ABO=60°,
∴∠OBE=90°-60°=30°,
∵BE=AB,OB=AB,
∴OB=BE,
∴∠BOE=$\frac{1}{2}$(180°-30°)=75°,
∵∠BOC=180°-60°=120°,
∴∠COE=120°-75°=45°.
点评 本题考查了矩形的性质、等边三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.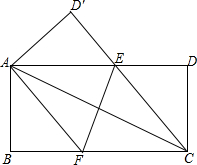 如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
(1)求EC的长度;
(2)证明:四边形AFCE是菱形.
 如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处(1)求EC的长度;
(2)证明:四边形AFCE是菱形.
10.下表是明明商行某商品的销售情况,该商品原价为560元,随着不同幅度的降价.
(1)每降价5元,日销量增加多少件?请你估计降价之前的日销量是多少?
(2)写出降价x(元)与日销量y(件)之间的关系式.
| 降价(单位:元) | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| 日销量(单位:件) | 780 | 810 | 840 | 870 | 900 | 930 | 960 |
(2)写出降价x(元)与日销量y(件)之间的关系式.
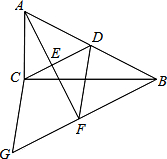 如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD平行线,交AE的延长线于点F,在延长线上截得FG=CD,连结CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于20.
如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD平行线,交AE的延长线于点F,在延长线上截得FG=CD,连结CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于20.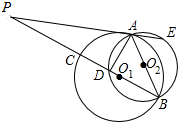 如图,已知⊙O1与⊙O2相交于A,B两点,AB是⊙O2的直径,过A点作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P,PB分别与⊙O1,⊙O2交于C,D两点,求证:
如图,已知⊙O1与⊙O2相交于A,B两点,AB是⊙O2的直径,过A点作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P,PB分别与⊙O1,⊙O2交于C,D两点,求证: